数据结构与算法 ​

数据结构 ​

数据结构(data structure)是带有结构特性的数据元素的集合，正确的数据结构选择可以提高算法的效率。

数据结构分为逻辑结构和物理结构。

• 逻辑结构：指数据元素之间逻辑关系的数据结构，这里的逻辑关系是指数据元素之间的前后间关系，与数据在计算机中的存储位置无关。
• 物理结构：指数据的逻辑结构在计算机存储空间中的存放形式称为数据的物理结构，也叫做存储结构。

数据的逻辑结构主要分为线性结构和非线性结构。

• 线性结构：数据结构的元素之间存在一对一线性关系，所有结点都最多只有一个直接前趋结点和一个直接后继结点。常见的有数组、队列、链表、栈。
• 非线性结构：各个结点之间具有多个对应关系，一个结点可能有多个直接前趋结点和多个直接后继结点。常见的有多维数组、广义表、树结构和图结构等。

数据的物理结构（以后我都统一称存储结构），表示数据元素之间的逻辑关系，一种数据结构的逻辑结构根据需要可以表示成多种存储结构，常用的存储结构有：

• 顺序存储：存储顺序是连续的，在内存中用一组地址连续的存储单元依次存储线性表的各个数据元素。
• 链式存储：在内存中的存储元素不一定是连续的，用任意地址的存储单元存储元素，元素节点存放数据元素以及通过指针指向相邻元素的地址信息。
• 索引存储：除建立存储结点信息外，还建立附加的索引表来标识节点的地址。索引表由若干索引项组成。
• 散列存储：又称 Hash 存储，由节点的关键码值决定节点的存储地址。

常用的 8 种数据结构：数组、队列、链表、散列、堆、栈、树、图

数组 ​

数组（Array）是由相同类型的元素（element）的集合所组成的数据结构，分配一块连续的内存来存储。利用元素的索引（index）可以计算出该元素对应的存储地址。

• 一维数组

const arr = [1, 2, 3];

const arr = [1, 2, 3];

• 二维数组 (矩阵)

const matrix = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9],
];

const matrix = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9],
];

队列 ​

队列（Queue）是先进先出（FIFO, First-In-First-Out）的线性表。在具体应用中通常用链表或者数组来实现。队列只允许在后端（称为 rear）进行插入操作，在前端（称为 front）进行删除操作。

class Queue {
    constructor() {
        this.list = [];
    }
    add(value) {
        this.list.unshift(value); // 先进
        return this.list;
    }
    get() {
        return this.list.pop(); // 先出
    }
}

class Queue {
    constructor() {
        this.list = [];
    }
    add(value) {
        this.list.unshift(value); // 先进
        return this.list;
    }
    get() {
        return this.list.pop(); // 先出
    }
}

链表 ​

链表（LinkedList）是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储，链表在插入的时候可以达到 O(1)的复杂度，但是查找一个节点或者访问特定编号的节点则需要 O(n)的时间。

应用：链表用来构建许多其它数据结构，如堆栈，队列和他们的派生。

常见的链表结构：

• 单向链表

class SingleLinkNode {
    constructor(value, next) {
        this.value = value; // 值
        this.next = next || null; // 后节点
    }
}

class SingleLinkNode {
    constructor(value, next) {
        this.value = value; // 值
        this.next = next || null; // 后节点
    }
}

• 双向链表

class DoubleLinkNode {
    constructor(value, prev, next) {
        this.value = value; // 值
        this.prev = prev || null; // 前节点
        this.next = next || null; // 后节点
    }
}

class DoubleLinkNode {
    constructor(value, prev, next) {
        this.value = value; // 值
        this.prev = prev || null; // 前节点
        this.next = next || null; // 后节点
    }
}

• 循环链表

栈 ​

栈（Stack）是一种数据呈线性排列的数据结构，和队列相反，栈的特点先进后出、后进先出，就是常说的 LIFO（Last in First Out）， 类似枪械弹夹的子弹先进后出原理。

class Stack {
    constructor() {
        this.list = [];
    }
    add(value) {
        this.list.unshift(value); // 后进
        return this.list;
    }
    get() {
        return this.list.shift(); // 先出
    }
}

class Stack {
    constructor() {
        this.list = [];
    }
    add(value) {
        this.list.unshift(value); // 后进
        return this.list;
    }
    get() {
        return this.list.shift(); // 先出
    }
}

栈的简单示意图：

树 ​

树（Tree）是由 n（n>0）个有限节点组成一个具有层次关系的集合。

结构特点是：

• 每个节点都只有有限个子节点或无子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树；
• 树里面没有环路(cycle)

简单示意图：

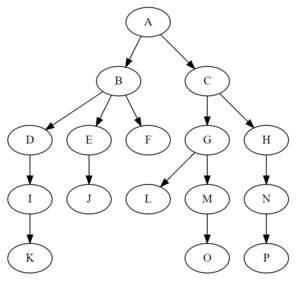
常见的典型树数据结构有：

• 二叉树：

  每个单元称为一个节点(node)，每个节点有 0 到两个子节点。

  js

  class TreeNode {
      constructor(value, left, right) {
          this.value = value;
          this.left = left || null;
          this.right = right || null;
      }
  }

  class TreeNode {
      constructor(value, left, right) {
          this.value = value;
          this.left = left || null;
          this.right = right || null;
      }
  }

  1
  2
  3
  4
  5
  6
  7
  

• 二叉查找树 (二叉搜索树 排序二叉树)：

  是指一棵空树或者具有下列性质的二叉树：

  • 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
  • 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
  • 任意节点的左、右子树也分别为二叉查找树；

• 平衡二叉查找树 (平衡二叉搜索树 AVL树)：

  任何节点两个子树的高度最大差别为 1，所以也被称作高度平衡树。AVL 树中，其最坏和平均的查找时间均为 O(logN)。

• 红黑树:

  是一种自平衡二叉查找树，是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。性质:

  • 节点是红色或黑色。
  • 根是黑色。
  • 所有叶子都是黑色（叶子是 NIL 节点）。
  • 每个红色节点必须有两个黑色的子节点。（或者说从每个叶子到根的所有路径上不能有两个连续的红色节点。）（或者说不存在两个相邻的红色节点，相邻指两个节点是父子关系。）（或者说红色节点的父节点和子节点均是黑色的。）
  • 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

• 完全二叉树： 一种很”饱满“的树，它的所有节点尽可能从上到下、从左到右地将每层都填满。

散列表 ​

散列表（Hash）又叫哈希表，存储的是由键(key)和值(value)组成的数据，根据键直接访问存储在内存存储位置的数据结构。

let hash1 = new Map();
let hash2 = new Object();

let hash1 = new Map();
let hash2 = new Object();

堆 ​

堆（Heap）比较特殊，是一种图的树形结构。被用于实现“优先队列”(priority queues)，优先队列是一种数据结构，可以自由添加数据，但取出数据时要从最小值开始按顺 序取出。在堆的树形结构中，各个顶点被称为“结点”(node)，数据就存储在这些结点中。

只要满足下面两个特点的树形结构就是堆：

• 堆是一个完全二叉树（所谓完全二叉树就是除了最后一层其他层的节点个数都是满的）。
• 堆中每一个节点的值都必须大于等于或者小于其子树中每一个节点的值。

应用：堆（通常是二叉堆）常用于排序。这种算法称作堆排序。

图 ​

图（Graph）是相对复杂的一种数据结构，由顶点和连接每对顶点的边所构成的图形就是图。

简单示意图

参考资料 ​

• 十三张图带你彻底了解所有数据结构
• 维基百科-数据结构